MATLAB Assignment 4 Solution

NJIT Math 222

Fourth MATLAB Assignment

Computational project part 1

I ran the code with \(N=10000\), \(\gamma=1\) and \(\beta\) varying. The assignment says to expect different behavior depending on whether or not \(R_0>1\), where \(R_0 = \frac{\beta N}{\gamma}\).

For these values of \(N\) and \(\gamma\), this an epidemic when \(\beta> 10^{-4}\). Therefore I tried three values of \(\beta\): \(2\times 10^{-4}\), \(1.25\times 10^{-4}\), and \(9\times10^{-5}\). For the first two values, I saw growth, with a larger epidemic in the first case \(\beta= 2\times10^{-4}\).

My results are in a MATLAB-generated webpage . This was generated from this MATLAB code .

Computational project part 2

Here you were asked to use phase-plane drawing software to examine solutions graphically. It was pointed out that \(\frac{dI}{dt}=0\) when \(S^* = \frac{\gamma}{\beta}\). From the following three images, we see that \(S_0> S^*\) when \(\beta>10^{-4}\), which is when we see epidemics.

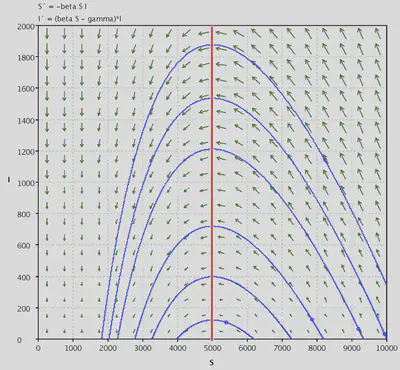
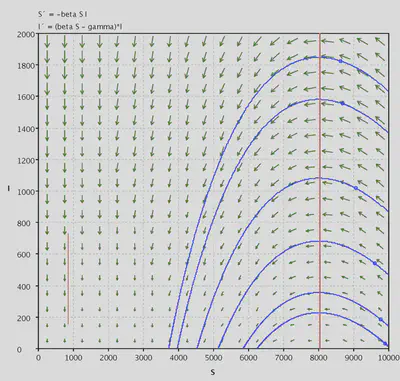
In the third case, \(\beta=9\times10^{-5}\) \(S_0=11111>N=10000\), so the infection number is decreasing at \(t=0\).

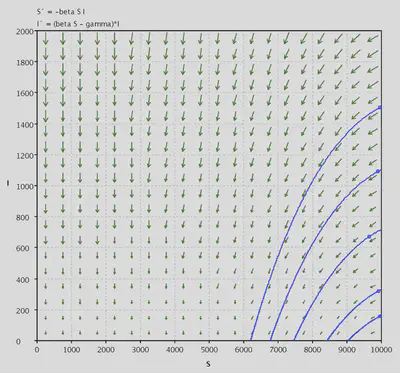
There is also a question asked “Can this model support a sustained epidemic.” The answer is that it cannot. In a sustained epidemic, the infection rate \(I(t)\) would have to reach a nonzero steady state but the phase plane shows that \(\lim_{t\to\infty}I(t)=0\) for all solutions, so it can’t sustain an epidemic. To support a sustained epidemic, a model must refresh its supply of susceptible individuals. Fortunately for the germs, we do that anyway by having babies! A more complete models will include births.