Abstract
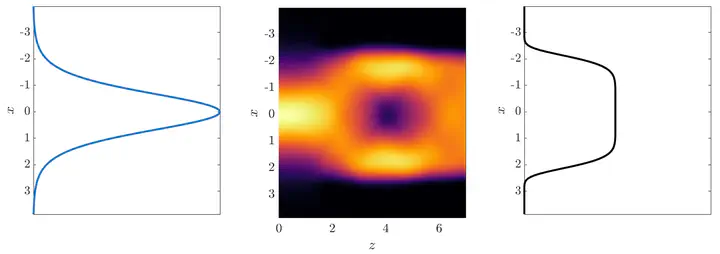
We address the problem of reshaping light in the Schrödinger optics regime from the perspective of optimal control theory. In technological applications, Schrödinger optics is often used to model a slowly-varying amplitude of a para-axially propagating electric field where the square of the waveguide’s index of refraction is treated as the potential. The objective of the optimal control problem is to find the controlling potential which, together with the constraining Schrödinger dynamics, optimally reshape the intensity distribution of Schrödinger eigenfunctions from one end of the waveguide to the other. This work considers reshaping problems found in work due to Kunkel and Leger, and addresses computational needs by adopting tools from the quantum control literature. The success of the optimal control approach is demonstrated numerically.
Jimmie Adriazola
NSF MPS-Ascend Postdoctoral Fellow, SMU.
In addition to studying applied mathematics and physics, Jimmie plays jazz guitar in local venues.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference