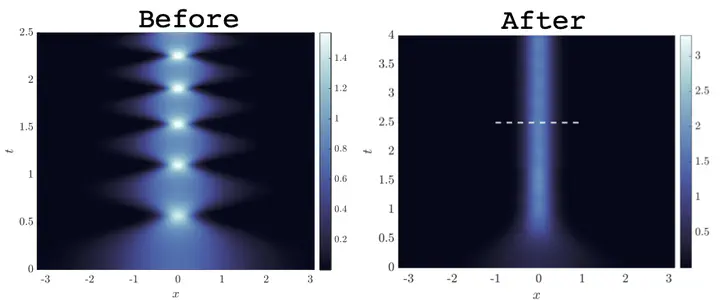
Abstract
Applications of Bose-Einstein Condensates (BEC) often require that the condensate be prepared in a specific complex state. Optimal control is a reliable framework to prepare such a state while avoiding undesirable excitations, and, when applied to the time-dependent Gross-Pitaevskii Equation (GPE) model of BEC in multiple space dimensions, results in a large computational problem. We propose a control method based on first reducing the problem, using a Galerkin expansion, from a PDE to a low-dimensional Hamiltonian ODE system. We then apply a two-stage hybrid control strategy. At the first stage, we approximate the control using a second Galerkin-like method known as CRAB to derive a finite-dimensional nonlinear programming problem, which we solve with a differential evolution (DE) algorithm. This search method then yields a candidate local minimum which we further refine using a variant of gradient descent. This hybrid strategy allows us to greatly reduce excitations both in the reduced model and the full GPE system.
Jimmie Adriazola
NSF MPS-Ascend Postdoctoral Fellow, SMU.
In addition to studying applied mathematics and physics, Jimmie plays jazz guitar in local venues.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference