Efficient Manipulation of Bose-Einstein Condensates in a Double-Well Potential
Abstract
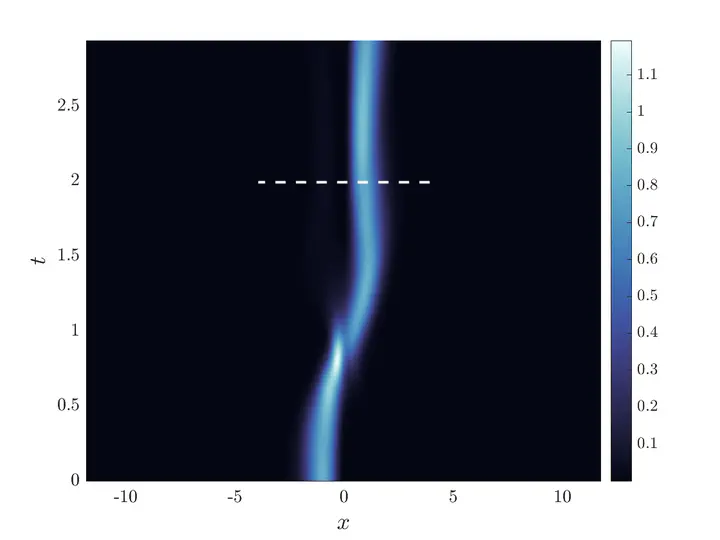
We pose the problem of transferring a Bose-Einstein Condensate (BEC) from one side of a double-well potential to the other as an optimal control problem for determining the time-dependent form of the potential. We derive a reduced dynamical system using a Galerkin truncation onto a finite set of eigenfunctions and find that including three modes suffices to effectively control the full dynamics, described by the Gross-Pitaevskii model of BEC. The functional form of the control is reduced to finite dimensions by using a Galerkin-type method called the chopped random basis (CRAB) method, which is then optimized by a genetic algorithm called differential evolution (DE). Finally, we discuss the the extent to which the reduction-based optimal control strategy can be refined by means of including more modes in the Galerkin reduction.
Jimmie Adriazola
Presidential Postdoctoral Fellow, Arizona State University
In addition to studying applied mathematics and physics, Jimmie plays jazz guitar in local venues.
