Chaotic scattering in solitary wave interactions: A singular iterated-map description

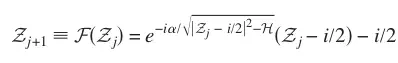
Abstract

We derive a family of singular iterated maps—closely related to Poincaré maps—that describe chaotic interactions between colliding solitary waves. The chaotic behavior of such solitary-wave collisions depends on the transfer of energy to a secondary mode of oscillation, often an internal mode of the pulse. This map allows us to go beyond previous analyses and to understand the interactions in the case when this mode is excited prior to the first collision. The map is derived using Melnikov integrals and matched asymptotic expansions and generalizes a multipulse Melnikov integral. It allows one to find not only multipulse heteroclinic orbits, but exotic periodic orbits. The maps exhibit singular behavior, including regions of infinite winding. These maps are shown to be singular versions of the conservative Ikeda map from laser physics and connections are made with problems from celestial mechanics and fluid mechanics

Roy Goodman

Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences

My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference