High-Order Bisection Method for Computing Invariant Manifolds of Two-Dimensional Maps

Roy Goodman and Jacek Wróbel. International Journal of Bifurcation and Chaos, 2011.
Jan 1, 2011·
Roy Goodman
Roy Goodman
Jacek Wróbel
Jacek Wróbel
· 1 min read
Abstract
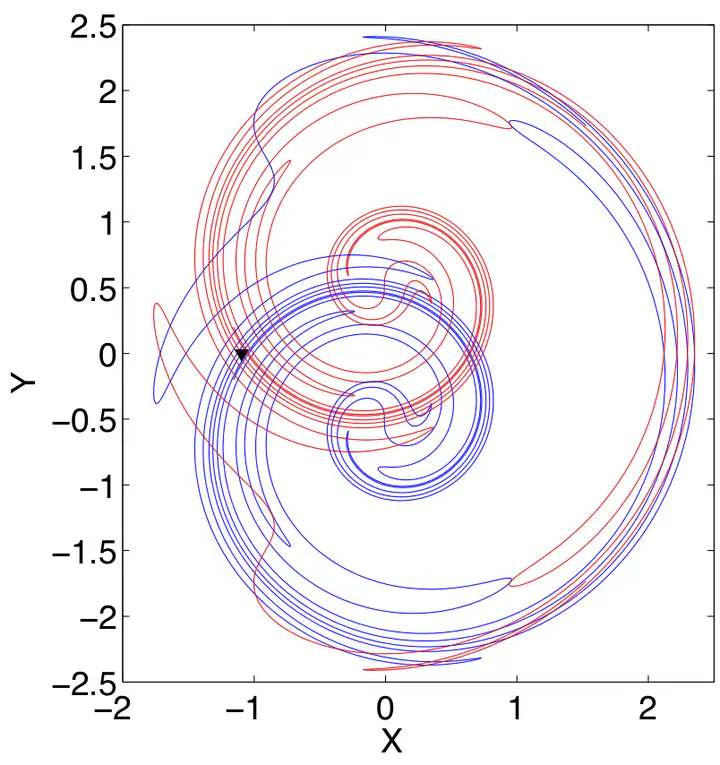
We describe an efficient and accurate numerical method for computing smooth approximations to invariant manifolds of planar maps, based on geometric modeling ideas from Computer Aided Geometric Design (CAGD). The unstable manifold of a hyperbolic fixed point is modeled by a piecewise Bézier interpolant (a Catmull–Rom spline) and properties of such curves are used to define a rule for adaptively adding points to ensure that the approximation resolves the manifold to within a specified tolerance. Numerical tests on a variety of example mappings demonstrate that the new method produces a manifold of a given accuracy with far fewer calls to the map, compared with previous methods. A brief introduction to the relevant ideas from CAGD is provided.
Type
Publication
International Journal of Bifurcation and Chaos, 21(07), 2017–2042
publication published

Part 1 of Jacek Wróbel’s dissertation.

Invariant manifold computation
Roy Goodman
Authors
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences

I am a professor in the Department of Mathematical Sciences at NJIT. My research applies methods of dynamical systems to (conservative, dispersive) nonlinear wave equations arising, for example, in optics and fluid mechanics. I am interested in dynamical and bifurcation phenomena, and I use techniques from Hamiltonian mechanics and perturbation theory, as well as extensive computations. My current research in vortex dynamics is supported by the NSF under DMS-2206016.

I led the effort to start the SIAM New York-New Jersey-Pennsylvania Section (SIAM NNP) and was its first president in 2023-2024. I have handed over the reins to a new leadership group.

Jacek Wróbel
Authors
Jacek Wróbel
Member of Technical Staff, Draper Laboratories

Jacek is a simulation engineer at Draper Labs in Cambridge, MA.

After completing his Ph.D. under the supervision of Roy Goodman, Jacek spent a year as a postdoc at NJIT working with Michael Booty and Michael Siegel. He spent three years as a postdoc at Tulane University with Lisa Fauci and Ricardo Cortez. He worked at Raytheon before beginning his current job as member of technical staff at Draper Laboratories.