Abstract
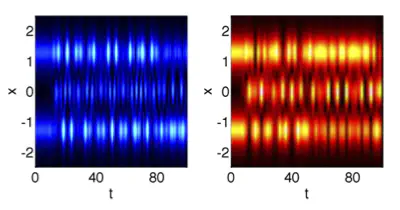
We examine the dynamics of solutions to nonlinear Schrödinger/Gross– Pitaevskii equations that arise due to semisimple indefinite Hamiltonian Hopf bifurcations—the collision of pairs of eigenvalues on the imaginary axis. We construct localized potentials for this model which lead to such bifurcations in a predictable manner. We perform a formal reduction from the partial differential equations to a small system of ordinary differential equations. We analyze the equations to derive conditions for this bifurcation and use averaging to explain certain features of the dynamics that we observe numerically. A series of careful numerical experiments are used to demonstrate the phenomenon and the relations between the full system and the derived approximations.
Erratum: At the end of section 2.4.3, top of page 10, I state that “a straightforward calculation” shows that the HH bifurcation studied by Johansson for the periodic NLS trimer to come from a semisimple -1:1 resonance. In fact, it is the generic non-semisimple bifurcation.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference