Abstract
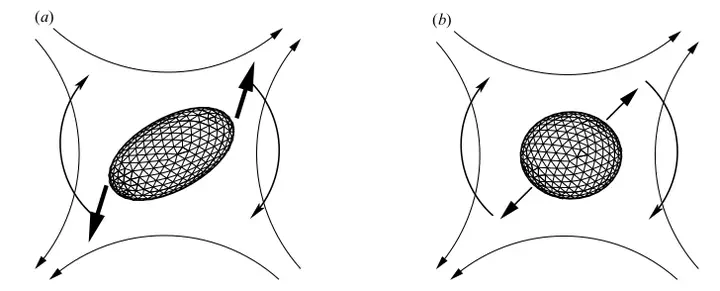
We investigate nonlinear phenomena in dispersed two-phase systems under creeping-flow conditions. We consider nonlinear evolution of a single deformed drop and collective dynamics of arrays of hydrodynamically coupled particles. To explore physical mechanisms of system instabilities, chaotic drop evolution, and structural transitions in particle arrays we use simple models, such as small-deformation equations and effective-medium theory. We find numerical and analytical solutions of the simplified governing equations. The small-deformation equations for drop dynamics are analyzed using results of dynamical systems theory. Our investigations shed new light on the dynamics of complex fluids, where the nonlinearity often stems from the evolving boundary conditions in Stokes flow.
Yuan-Nan Young
Professor
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference