Abstract
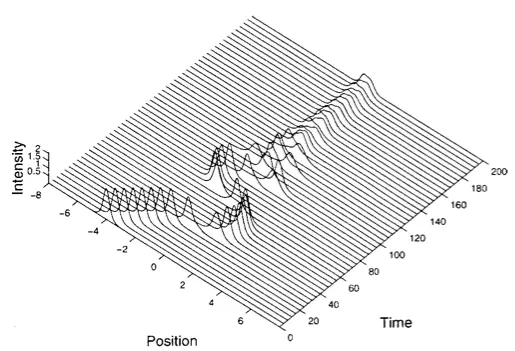
Gap solitons are localized nonlinear coherent states that have been shown both theoretically and experimentally to propagate in periodic structures. Although theory allows for their propagation at any speed v, between 0 and c, they have been observed in experiments at speeds of approximately 50% of c. It is of scientific and technological interest to trap gap solitons. We first introduce an explicit multiparameter family of periodic structures with localized defects, which support linear defect modes. These linear defect modes are shown to persist into the nonlinear regime, as nonlinear defect modes. Using mathematical analysis and numerical simulations, we then investigate the capture of an incident gap soliton by these defects. The mechanism of capture of a gap soliton is resonant transfer of its energy to nonlinear defect modes. We introduce a useful bifurcation diagram from which information on the parameter regimes of gap-soliton capture, reflection, and transmission can be obtained by simple conservation of energy and resonant energy transfer principles.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference
