Topological features determining the error in the inference of networks using transfer entropy
Abstract
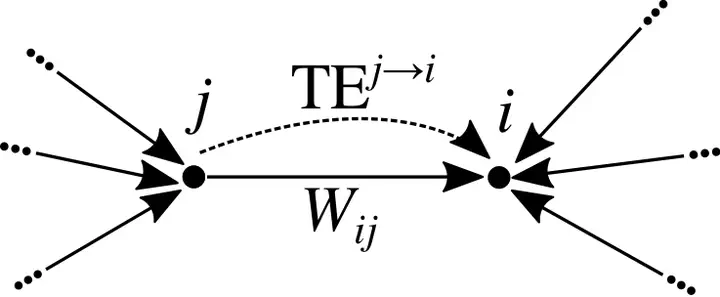
The problem of inferring interactions from observations of individual behavior in networked dynamical systems is ubiquitous in science and engineering. From brain circuits to financial networks, there is a dire need for robust methodologies that can unveil network structures from individual time series. Originally formulated to identify asymmetries in pairs of coupled dynamical systems, transfer entropy has been proposed as a model-free, computationally-inexpensive framework for network inference. While previous studies have cataloged a library of pathological instances in which transfer entropy-based network reconstruction can fail, we presently lack analytical results that can help quantify the accuracy of the identification and pinpoint scenarios where false inferences results are more likely to be registered. Here, we present a detailed analytical study of a Boolean network model of policy diffusion. Through perturbation theory, we establish a closed-form expression for the transfer entropy between any pair of nodes in the network up to the third order in an expansion parameter that is associated with the spontaneous activity of the nodes. While for slowly-varying dynamics transfer entropy is successful in capturing the weight of any link, for faster dynamics the error in the inference is controlled by local topological features of the node pair. Specifically, the error in the inference of a weight between two nodes depends on the mismatch between their weighted in-degrees that serves as a common uncertainty bath upon which we must tackle the inference problem. Interestingly, an equivalent result is discovered when numerically studying a network of coupled chaotic tent maps, suggesting that heterogeneity in the in-degree is a critical factor that can undermine the success of transfer entropy-based network inference.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference
