Loss of Physical Reversibility in Reversible Systems
Abstract
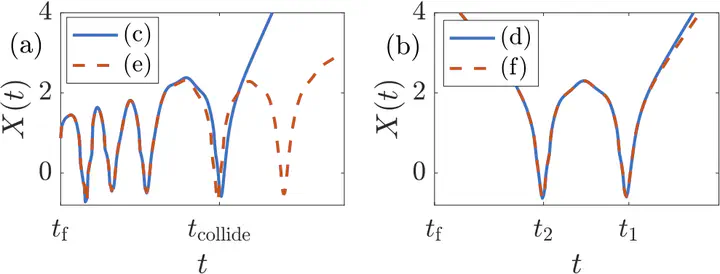
A dynamical system is said to be reversible if, given an output, the input can always be recovered in a well-posed manner. Nevertheless, we argue that reversible systems that have a time-reversal symmetry, such as the Nonlinear Schrödinger equation and the phi-4 equation can become physically irreversible. By this, we mean that realistically-small experimental errors in measuring the output can lead to dramatic differences between the recovered input and the original one. The loss of reversibility reveals a natural arrow of time, reminiscent of the thermodynamic one, which is the direction in which the radiation is emitted outward. Our results are relevant to imaging and reversal applications in nonlinear optics.
Type
Publication
Physica D: Nonlinear Phenomena, 410, 132515
Authors
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
I am a professor in the Department of Mathematical Sciences at NJIT. My research applies methods of dynamical systems to (conservative, dispersive) nonlinear wave equations arising, for example, in optics and fluid mechanics. I am interested in dynamical and bifurcation phenomena, and I use techniques from Hamiltonian mechanics and perturbation theory, as well as extensive computations. My current research in vortex dynamics is supported by the NSF under DMS-2206016.
I led the effort to start the SIAM New York-New Jersey-Pennsylvania Section (SIAM NNP) and was its first president in 2023-2024. I have handed over the reins to a new leadership group.
