MATLAB Project 2 Solution

NJIT Math 222

Problem 1

Consider the differential equation $$\frac{dx}{dt}=f(x)=\sin x-a\sin 4x$$ We will look at four different values $a=0.2,a=0.4,a=0.8,a=1$.

Graphs below were drawn with Desmos and direction fields with the Slopes App.

The case $\mathbf{a}\mathbf{=}\mathbf{0.2}$

The graph of $f(x)$ looks like a slightly wigglier version of $\sin (x)$ and, more importantly, has the same zeros. Stable equilibrium are marked in blue and unstable in purple.

The direction field looks very similar to that of $\sin x$:

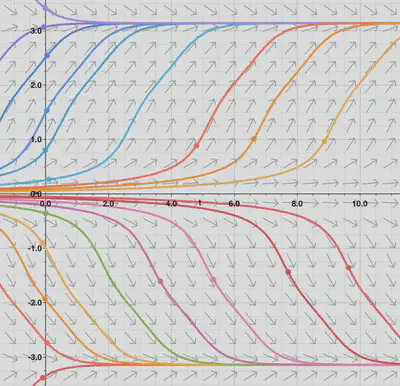
The case $\mathbf{a}\mathbf{=}\mathbf{0.4}$

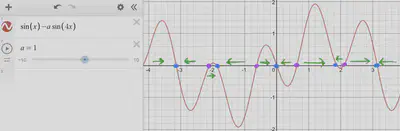
Two new zeros have arisen on either side of $x=0$. Note that the equilibrium at zero has become stable while the two new equilibria are unstable. In fact, these two new equilibria exist for all $a>\frac{1}{4}$.

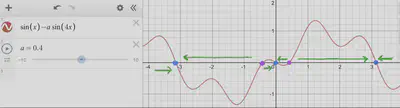
We can see in the direction field regions where the direction of the flow is reversed compared to the previous one.

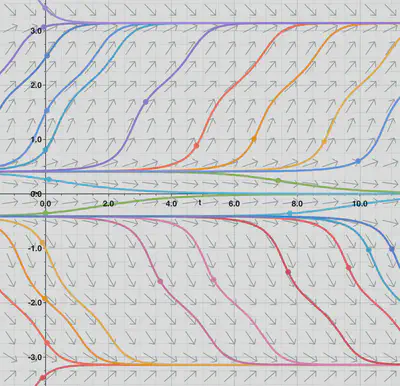
The case $\mathbf{a}\mathbf{=}\mathbf{0.8}$

Not much has changed here compared with the previous case, however the curves come very close to the $x$-axis near $x=\pm 2$. Watch this space, as things will change near here in the final case

We can also see that trajectories slow down near $x=\pm 2$ as seen from the slopes.

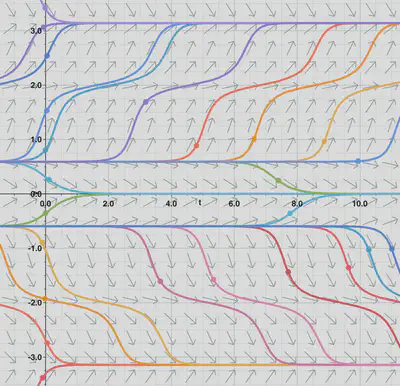
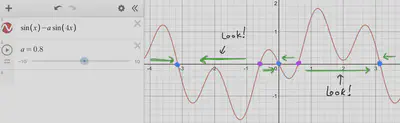
The case $\mathbf{a}\mathbf{=}\mathbf{1}$

Four new fixed points have arisen in pairs near $x=\pm 2$. In fact, with some fancier math we can find that the critical value is $a=\frac{1}{4}(\frac{11}{\sqrt{6}}-\sqrt{\frac{2}{3}})\approx 0.919$.

In the direction field, we can see new types of trajectories of the opposite slope near $x=\pm 2$ in addition to four new fixed points.

Problem 2

Graph the direction field and some solutions for the non-autonomous equation $$\frac{dx}{dt}=x-\frac{tx}{1+x^2}.$$

The direction field looks like this:

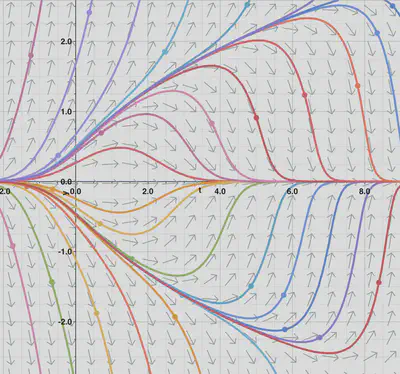
Solutions can either go to zero as $t\to \mathrm{\infty }$ or they can go to $\pm \mathrm{\infty }$. There is a pair of curves separating these two regimes of behavior, but I haven’t been able to figure out a formula for it.