Abstract
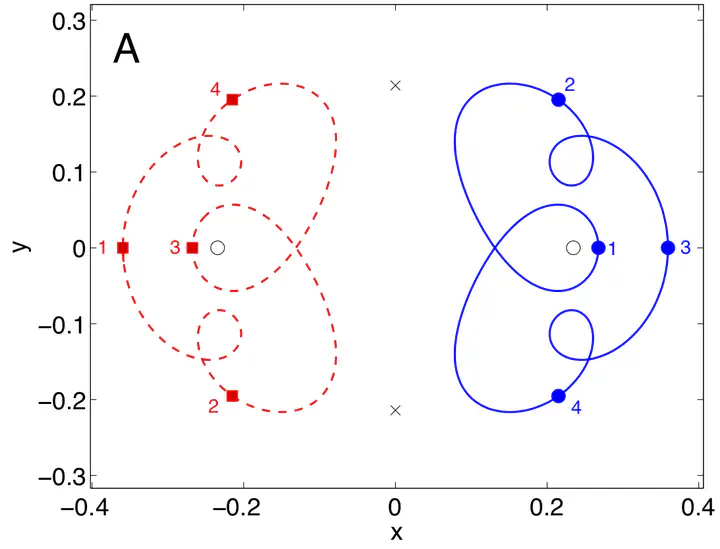
We study the motion of a vortex dipole in a Bose-Einstein condensate confined to an anisotropic trap. We focus on a system of ordinary differential equations describing the vortices’ motion, which is in turn a reduced model of the Gross-Pitaevskii equation describing the condensate’s motion. Using a sequence of canonical changes of variables, we reduce the dimension and simplify the equations of motion. We uncover two interesting regimes. Near a family of periodic orbits known as guiding centers, we find that the dynamics is essentially that of a pendulum coupled to a linear oscillator, leading to stochastic reversals in the overall direction of rotation of the dipole. Near the separatrix orbit in the isotropic system, we find other families of periodic, quasi-periodic, and chaotic trajectories. In a neighborhood of the guiding center orbits, we derive an explicit iterated map that simplifies the problem further. Numerical calculations are used to illustrate the phenomena discovered through the analysis. Using the results from the reduced system we are able to construct complex periodic orbits in the original, partial differential equation, mean-field model for Bose-Einstein condensates, which corroborates the phenomenology observed in the reduced dynamical equations.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference
Panos Kevrekidis
Professor
