Abstract
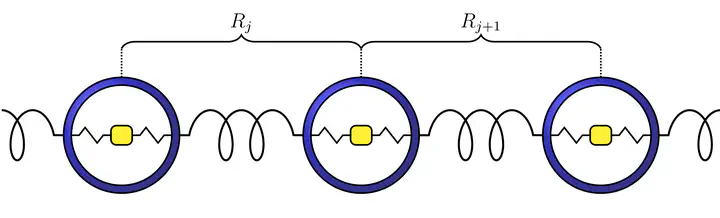
We consider the existence of spatially localized traveling wave solutions of the mass-in-mass lattice. Under an anti-resonance condition first discovered by Kevrekidis, Stefanov and Xu, we prove that such solutions exist in two distinguished limits, the first where the mass of the internal resonator is small and the second where the internal spring is very stiff. We then numerically simulate the solutions and these simulations indicate that the anti-resonant traveling waves are weakly unstable.
Type
Publication
Z. Angew. Math. Phys.
Timothy Faver
Assistant Professor
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference
