Abstract
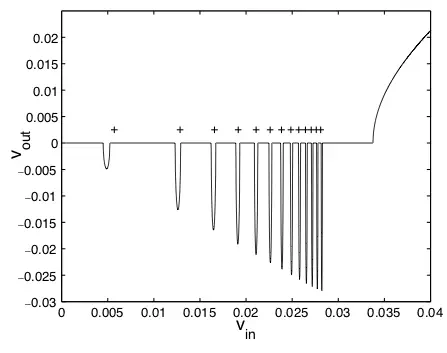
A model of soliton–defect interactions in the sine-Gordon equations is studied using singular perturbation theory. Melnikov theory is used to derive a critical velocity for strong interactions, which is shown to be exponentially small for weak defects. Matched asymptotic expansions for nearly heteroclinic orbits are constructed for the initial value problem, which are then used to derive analytical formulas for the locations of the well known two- and three-bounce resonance windows, as well as several other phenomena seen in numerical simulations.
Type
Publication
Physica D
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference
