Abstract
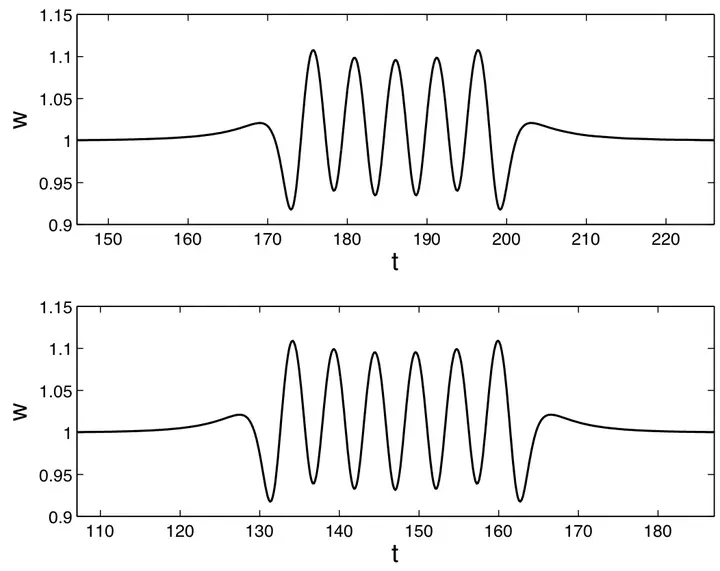
We consider the interactions of two identical, orthogonally polarized vector solitons in a nonlinear optical fiber with two polarization directions, described by a coupled pair of nonlinear Schrödinger equations. We study a low-dimensional model system of Hamiltonian ordinary differential equations (ODEs) derived by Ueda and Kath and also studied by Tan and Yang. We derive a further simplified model which has similar dynamics but is more amenable to analysis. Sufficiently fast solitons move by each other without much interaction, but below a critical velocity the solitons may be captured. In certain bands of initial velocities the solitons are initially captured, but separate after passing each other twice, a phenomenon known as the two-bounce or two-pass resonance. We derive an analytic formula for the critical velocity. Using matched asymptotic expansions for separatrix crossing, we determine the location of these ``resonance windows.’’ Numerical simulations of the ODE models show they compare quite well with the asymptotic theory.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference
