Abstract
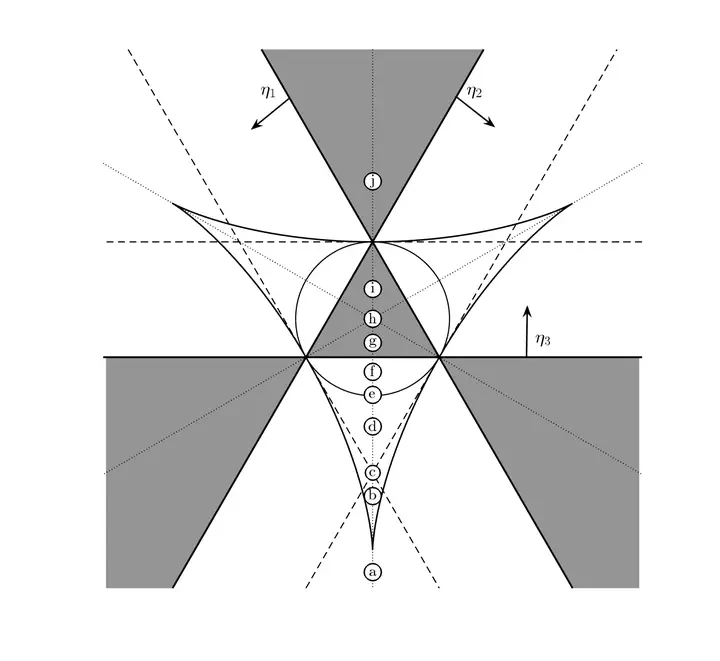
We derive a symplectic reduction of the evolution equations for a system of three point vortices and use the reduced system to succinctly explain a kind of bifurcation diagram that has appeared in the literature in a form that was difficult to understand and interpret. Using this diagram, we enumerate and plot all the global phase-space diagrams that occur as the circulations of the three vortices are varied. The reduction proceeds in two steps: a reduction to Jacobi coordinates and a Lie-Poisson reduction. In a recent paper, we used a different method in the second step. This took two forms depending on a sign that arose in the calculation. The Lie-Poisson equations unify these into a single form. The Jacobi coordinate reduction fails when the total circulation vanishes. We adapt the reduction method to this case and show how it relates to the non-vanishing case.
Atul Anurag (अतुल अनुराग)
Graduate Student
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference