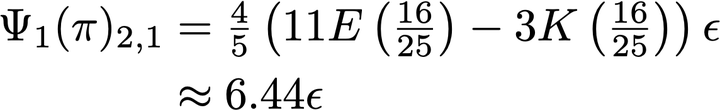Abstract
The point-vortex system is a system of longstanding interest in nonlinear dynamics, describing the motion of a two-dimensional inviscid fluid that is irrotational except at a discrete set of moving point vortices, at which the vorticity diverges. The leapfrogging orbit consists of two rotating pairs of like-signed vortices which, taken as a quartet, propagate at constant velocity. It is known that if the two pairs are initially widely separated, the motion is stable, while if they are closer together it becomes unstable, with this relation represented by a dimensionless parameter $\alpha$ defined in the text. We here demonstrate analytically that the transition from stability to instability happens at a critical value $\alpha = \phi^{-2}$, where $\phi$ is the golden ratio. This value had been hypothesized based on careful numerics by Tophøj and Aref, and by the present authors using a semi-analytic argument but not previously demonstrated through exact analysis.
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference
Brandon Behring
Data Scientist, Prudential Insurance
Brandon defended his dissertation on leapfrogging point vortices in August 2020 He spent about a year as a postdoc in the Dynamical Systems Laboratory at the NYU Tandon School of NYU. He is now a data scientist at Prudential Insurance, and has a very cute baby girl.