Mathematical Analysis of Fractal Kink-Antikink Collisions in the $\varphi^4$ Model
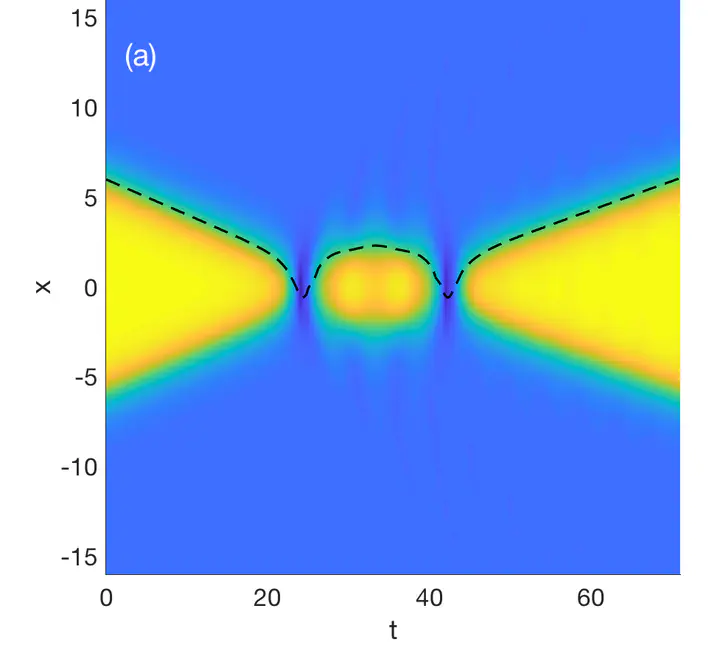
Abstract
We analyze the fractal structure seen in kink-antikink collisions of the $\varphi^4$ equation. The analysis is based on qualitative ordinary differential equation models related to those obtained using the variational approximation. We derive a discrete-time iterated map approximation to the dynamics, from which many features of the model ODE system may be derived. We discuss the problems with Sugiyama’s variational model that have been pointed out recently by Takyi and Weigel.
Type
Publication
A Dynamical Perspective on the $\varphi^4$ Model
Roy Goodman
Professor, Associate Chair for Graduate Studies, Department of Mathematical Sciences
My research interests include dynamical systems and nonlinear waves, vortex dynamics, quantum graphs, and network inference