Stability and instability of nonlinear defect states in the coupled mode equations---analytical and numerical study
Abstract
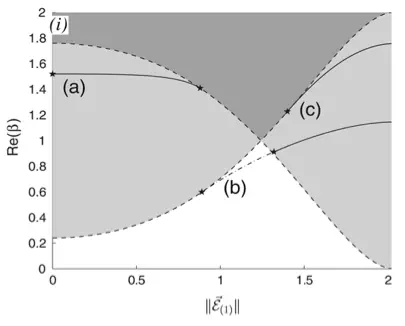
Coupled backward and forward wave amplitudes of an electromagnetic field propagating in a periodic and nonlinear medium at Bragg resonance are governed by the nonlinear coupled mode equations (NLCME). This system of PDEs, similar in structure to the Dirac equations, has gap soliton solutions that travel at any speed between 0 and the speed of light. A recently considered strategy for spatial trapping or capture of gap optical soliton light pulses is based on the appropriate design of localized defects in the periodic structure. Localized defects in the periodic structure give rise to defect modes, which persist as nonlinear defect modes as the amplitude is increased. Soliton trapping is the transfer of incoming soliton energy to nonlinear defect modes. To serve as targets for such energy transfer, nonlinear defect modes must be stable. We therefore investigate the stability of nonlinear defect modes. Resonance among discrete localized modes and radiation modes plays a role in the mechanism for stability and instability, in a manner analogous to the nonlinear Schro ̈dinger/Gross–Pitaevskii (NLS/GP) equation. However, the nature of instabilities and how energy is exchanged among modes is considerably more complicated than for NLS/GP due, in part, to a continuous spectrum of radiation modes which is unbounded above and below. In this paper we (a) establish the instability of branches of nonlinear defect states which, for vanishing amplitude, have a linearization with eigenvalues embedded within the continuous spectrum, (b) numerically compute, using Evans function, the linearized spectrum of nonlinear defect states of an interesting multiparameter family of defects, and (c) perform direct time-dependent numerical simulations in which we observe the exchange of energy among discrete and continuum modes